Believe it or not, mathematics plays an important role in the field of sports. Coaches, athletes, trainers often use mathematics to gain a competitive advantage over their counterparts. With statistics of games, statistics of players, and probabilities of winning or losing games, mathematics is everywhere. Applications of calculus in sports are endless!
Calculus in sports: running races
How is mathematics involved in running? I know it surprises most of us. To optimize their run, runners must keep themselves at the right speed in order to finish in the shortest time possible. According to Joseph Keller’s, A Theory of Competitive Running, the physiological running capacity of a human body can be measured using a set of differential equations.
According to this theory, to win a running race under 291 meters, the optimum strategy is to sprint at 100% acceleration for the entire 291 meters. Races above 291 meters require a different strategy to optimize performance.
Finding the optimal velocity for the run while conserving energy
Keller’s theory, which is based on Newton’s second law and the calculus of variations, provides an optimum strategy for running one-lap and half-lap races. Keller wrote the equation of motion as:
\(\frac { d\upsilon }{ dt } +\frac { \upsilon }{ \tau } =f(t),\)where \(\upsilon\) is runner’s speed as a function of time t, \(\tau\) is a constant characterizing the resistance to running, assumed to be proportional to running speed, and \(f(t)\le F\) is the propulsive force per unit mass.
Empirical knowledge of human exercise physiology is expressed in the assumed relation between propulsive force and energy supply,
\(\frac { dE }{ dt } =\sigma -f\upsilon,\)where E represents the runner’s energy supply, which has a finite initial value \({ E }_{ 0 },\) and is replenished at a constant rate \(\sigma.\) In spite of this replenishment, the energy supply reaches zero at the end of the race. \(\tau,\) \(\sigma,\) \({ E }_{ 0 }\) and F are found by comparing the optimal race times. The use of calculus in sports does not end here, next let’s take a look at how it can be applied in baseball.
Calculus in baseball
In baseball, calculus can be used to optimize the pitcher’s throw to achieve maximum efficiency. Also, calculus can be used to calculate the projectile motion of baseball’s trajectory and to predict if runners can make it to the next base on time given their running speed and the speed of a hit ball.

Finding the work required to throw the baseball
The work done W on a moving ball from a position \({ s }_{ 0 }\) to \({ s }_{ 1 }\) is equal to the change in ball’s kinetic energy. The kinectic energy K of a baseball of mass m and velocity v is given by \(K=\frac { 1 }{ 2 } m{ v }^{ 2 }\).
\(W=\int _{ { s }_{ 0 } }^{ { s }_{ 1 } }{ F(s) } ds=\frac { 1 }{ 2 } m{ v }_{ 1 }^{ 2 }-\frac { 1 }{ 2 } m{ v }_{ 0 }^{ 2 }\)Where \({ v}_{ 0 }\) and \({ v }_{ 1 }\) are initial and final velocities. Using this, baseball players can figure out how much force they need to exert on the ball to reach the place where they want the ball to go.
Finding the Average force on the bat during the collision
The collision of ball and bat, are quite complex and their models are discussed in detail in a book by Robert Adair, The Physics of Baseball, (New York: HarperPerennial).
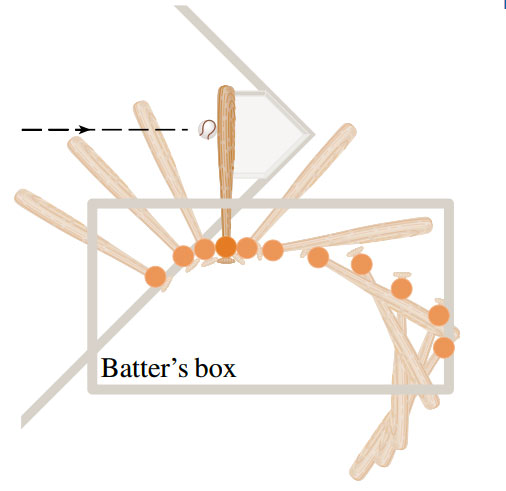
The above image shows an overhead view of the position of a baseball bat, shown every fiftieth of a second during a typical swing. We can calculate the average force on the bat during this collision by first calculating the change in the ball’s momentum.
We know that the momentum p of an object is the product of its mass m and its velocity v, that is, p=mv. Suppose an object, moving along a straight line, is acted on by a force F=F(t) which is a continuous function of time t.
The change in ball’s momentum over a time interval \([{ t }_{ 0 }-{ t }_{1 }]\) is equal to the integral of force F from time \({ t }_{ 0 }\) to \({ t }_{ 1 }\).
\(p({ t }_{ 1 })-p({ t }_{ 0 })=\int _{ { t }_{ 0 } }^{ { t }_{ 1 } }{ F(t) } dt\)Using the above formula, one can find the average force on the bat during the collision F=ma where \(a=\frac { \Delta v }{ t }\). The application of calculus in sports does not end with running and baseball, now let’s see how it can be applied in basketball too.
Calculus in basketball
Calculus can be used in basketball to find the exact arc length of a shot from the shooter’s hands to the basket. The moment the basketball is released from the shooter’s hands, its travelling path creates an arc all the way to the net.
Using the angle of release and strength of the release, one can mathematically predict the travelling path and the length of the arc. While the ball is in the air, it is affected by only one force, which is gravity!

Finding the arc length of a basketball throw
The travel path of a basketball can be divided into two components, the horizontal (x) direction and the vertical (y) direction. These two components can be represented by the following parametric equations:
For horizontal, \(x(t)={ x }_{ o }+{ v }_{ o } cos(\theta )t\)
For vertical, \(y(t)={ y }_{ o }+{ v }_{ o }sin(\theta )t+\frac { 1 }{ 2 } g{ t }^{ 2 }\)
where,
\({ x }_{ o }\) is the initial horizontal position of the basketball.
\({ y }_{ o }\) is the initial vertical position of the basketball.
\({ v }_{ o }\) is the initial velocity of the basketball.
\(\theta\) is the angle the ball is projected with respect to the x-axis.
g is the acceleration due to gravity, -9.81 m/\({ s. }^{ 2 }\)
t is the time travelled.
The derivatives of x(t) and y(t) with respect to time t are:
\(\frac { dx }{ dt } ={ v }_{ o }cos(\theta )t\) \(\frac { dy }{ dt } ={ v }_{ o }sin(\theta )-9.81t\)Now, the distance of the travel distance of the basketball can be found using the arc length equation:
\(L=\int _{ \alpha }^{ \beta }{ \sqrt { { (\frac { dx }{ dt } ) }^{ 2 }+({ \frac { dy }{ dt } ) }^{ 2 } } } dt,\alpha \le t\le \beta\)Now, by inserting the derivatives of x(t) and y(t) in the arc length equation:
\(L=\int _{ \alpha }^{ \beta }{ \sqrt { { ({ v }_{ o }cos(\theta )) }^{ 2 }+({ { v }_{ o }sin(\theta )-9.81t) }^{ 2 } } }dt\)This equation can be modified based on: \({ (a-b) }^{ 2 }={ a }^{ 2 }-2ab+{ b }^{ 2 }\) \(L=\int _{ \alpha }^{ \beta }{ \sqrt { { { { v }_{ o } }^{ 2 }{ cos }^{ 2 }(\theta ) }+{ { { v }_{ o } }^{ 2 }{ sin }^{ 2 }(\theta )-19.62\ast t\ast { v }_{ o }sin(\theta )+96.24{ t }^{ 2 } } } } dt\)
By further modifying, we can arrive at this formula:
\(L=\int _{ \alpha }^{ \beta }{ \sqrt { { { { v }_{ o } }^{ 2 }{ -19.62\ast t\ast { v }_{ o }sin }(\theta ) }+96.24{ { t }^{ 2 } } } } dt\)An example: If the average velocity of a basketball throw is 2.24 m/s, the angle of release is 45 degreees, and the time t required for the ball to travel is about 2 seconds, then the arc length can be calculated using the above formula:
\(L=\int _{ 0 }^{ 2 }{ \sqrt { { { 2.24 } }^{ 2 }{ -19.62\ast t\ast 2.24sin }(45)+96.24{ t }^{ 2 } } dt } = 17.34m\)
The above figure shows different angles and entry points of a basketball into a basketball hoop. The diameter of the hoop ring is 18 inches. As the basketball size is smaller than the hoop ring, there is always a constant hoop margin. Hoop margin is the amount of space left in the hoop ring after the basketball enters it.
Free throws, jump shots, and three-pointers enter at an angle that gives an oval entrance to the hoop. This changes the given hoop margin. Apparent hoop size is the apparent opening of the hoop to the ball. So, flatter the arc of throw, the smaller the ellipse of the hoop ring.
An apparent hoop margin is the apparent hoop size minus the basketball’s diameter. A basketball can be thrown in different ways and different angles. So, the apparent hoop margin varies with each shot.
Finding the velocity required for the basketball to enter the basket
One can also find the velocity required for the basketball shot given the height of the player’s throw and distance from the hoop. This is the equation for a player to shoot the basketball in order to make it enter the basket perfectly. [1]
\(f(x)=(\frac { -16 }{ { v }_{ 0 }^{ 2 }{ cos }^{ 2 }\alpha } ){ x }^{ 2 }+(tan\alpha )x+{ h }_{ 0 }\)where
\({ h }_{ 0 }\) is the height from which the ball is thrown. \(\alpha\) is the angle at which the ball is thrown. \({ v }_{ 0 }\) is the speed at which the ball is thrown. \(x\) is the distance the ball travels.And the formula for the range of a basketball trajectory is
\(Range=\frac { { v }_{ 0 }^{ 2 }sin(2\alpha ) }{ 32 }\)Once we know the range and the \(\alpha\) angle of throw, we can calculate the velocity required for the throw using the above formulae. [2]
The application of calculus in sports does not end with running, baseball and basketball. You can apply calculus to any physical sport to optimize performance. Share your thoughts with us in the comment section below.
Footnotes
1. Gablonsky, J. and Lang, A. (2005). Modeling Basketball Free Throws. Society for Industrial and Applied Mathematics, [online] 47(4), pp.775–798.
2. Barzykina, I. (2017). The physics of an optimal basketball free throw.